2021SMuK                      English Version                      Relativity

A method to measure the linear motion to the gravitational field.

Have we already understood relativity correctly? Dark matter is just as difficult to grasp as the properties of ether more than 100 years ago. Perhaps one has time to question Einstein's dogmas during the corona pandemic. In Einstein's sense, it means that you question what you currently think is right. In doing so, however, one must not put the question on the tracks that lead exactly to the result that confirms the dogmas.

At the very beginning I would like to ask the question: is the empty space really empty?

To clarify the question, let's imagine two rings of the same size parallel to each other. In order to use as little mass as possible, it should only be thin ring structures, away from other masses in a void. Observers sit at the edge of the rings. The rings rotate with respect to one another around their common axis. No centrifugal force is measured in one of the rings. The centrifugal force that should be measured at the edge of the other ring can be calculated from the size of the rings and the angular velocity.

But does a centrifugal force really have to be measured here and if so, what determines the size? Does that determine the mathematics, or is there something in the empty space here that produces the centrifugal force and thus also determines the size?

Regardless of mathematics or human imagination: When the experiment is carried out in real life, no centrifugal force is measured at the edge of the ring, which does not rotate towards the surrounding universe. A centrifugal force is measured in the ring that rotates for this purpose.

Imagine a ring rotating so fast that its edge moves at half the speed of light compared to a non-rotating ring. The observer sitting on the edge moves to the gravitational field at half the speed of light. Now he is breaking away from the ring. It thus moves tangentially away from the ring in a straight line. This corresponds to an inertial movement. According to the special theory of relativity, he can no longer move to the gravitational field, because then he could also rest for it and there would be a preferred state of rest. I don't want to go into more detail at this point. With the method shown below you can measure the movement to the gravitational field during rotation and thus also determine the state of rest. This must then also apply to the linear movement.

My question is: Is the empty space really empty, or is there a gravitational field to which you can then move in a straight line?

In order to get closer to the answer, a way is to be shown here that is only based on unambiguous events that must apply to every observer, regardless of how they move or where they are.

The meeting of two observers A and B with their watches is seen as a clear event. During this encounter, they compare their watches. The clock values ​​displayed apply to all observers. The information that they are receiving from space at this moment has also arrived at that moment for all other observers.

The causality is also clear for all observers, because everything that A and B experience afterwards has also happened for everyone else afterwards and everything that A and B have experienced before that has also happened for everyone else before. The sequence of events is the same for everyone. That is the basis for the idea of ​​world lines. How other observers classify these events in terms of their own time, and how great they measure the distance to these events, or the distance of such events from one another, depends on the setting of the measuring instruments for spatial simultaneity. This can be different for all observers, as it has not yet been possible to clearly determine it.

The relative proportions of the measurement results, measured with atomic clocks and light signals under Einstein's definition of simultaneity, undoubtedly correspond to the Lorentz transformations in the universe that surrounds us. In any case, no contradicting observations have been made so far. Math formulas are difficult to understand. It is even more difficult to see what the consequences are.

Unambiguous events are to be calculated based on an observer. Every observer who is moved to do this must then incorporate this into his measurements without contradictions occurring.

Let us come back to the experiment of two rings rotating parallel to each other, far removed from larger masses. No centrifugal force is measured at the edge of one of the rings. We want to describe this state as not circling.

Let us transfer the knowledge we have gained from satellite navigation and Universal Time Coordinated UTC to this experiment.

To measure the time, we use atomic clocks corresponding to the light clocks. At first we don't want to measure spatial distances. When measuring points that are spatially distant are moved, the measured value depends on the spatial simultaneity. This can only be limited causally within the framework of the world line of the fastest possible transfer of information, but cannot be clearly determined.

Here is a little excursion for those inexperienced in the matter:

Information is sent out, answered at a remote location and received again. Causally, the answering can only have happened after sending and before receiving again. It is not possible to determine when exactly it happened within this period of time.

The information could first have been sent by post, which takes a day, and then as a telegram, which takes only half an hour. But it could also be the other way around. In order to be able to narrow down when the answer could have happened, one has to know something about the transport of the information.

Let's take a sound signal and simply let it reflect in response, like an echo in the mountains. Then when did the reflection take place? Exactly half the time to get there and back? If there is a little wind, the sound signal took less time in the direction of the wind than in the opposite direction. Here, too, the point in time cannot be narrowed down with certainty.

What about light. Let's take a light signal. It's the fastest we have available. In response, we simply let this reflect too. But even that is not a clear-cut solution. As we can see in the example shown later, the speed measurement of a movement depends on the setting of spatial simultaneity. If only light clocks and light signals are used and each observer adjusts his measuring instruments for spatial simultaneity so that they correspond to Einstein's definition of simultaneity, then the results always merge for all observers. As will be shown later, this also applies entirely to rotation.

Back to the rings. Let us position the atomic clock A on the non-circling ring A at the observer A. On the ring B which is circling to the east in the sense of the earth's rotation, the atomic clock B at the observer B.

The atomic clocks should show the time according to the defined second. Then clock B went slower with every encounter with A. The seconds pass more slowly on all clocks that are positioned on rotating rings. The faster they circle, the slower the clocks go. The encounters between the clocks are unambiguous events. It follows from this that for observer B his clock B runs more slowly than clock A.

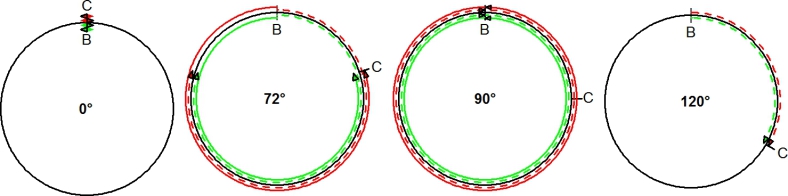
Now when they meet, A and B send out a flash of light that is supposed to spread in both directions along the rings. Then only in the case of the non-circling ring A do the lightning components moving in opposite directions reach the observer A from both directions at the same time. Light spreads with a uniform front. Nothing else has been observed in the universe so far. Then the lightning components cannot reach B moved to A from both directions at the same time. The lightning component that is propagating in the west direction, i.e. against the direction of movement of B, reaches B first and later the lightning component that is propagating in the east direction. This also corresponds to the findings from satellite navigation.

The observer should reflect the lightning components when they are reached by them. A thereby produces the reflections A(ew) and A(we) for all observers at the same time. These also reach A for all observers again at the same time.

B first generates the reflections B(we) from the lightning component that initially spread westward and then moves eastward after the reflection. Only a little later does the lightning component, which has moved in an easterly direction, reach B. With this he creates the reflection B(ew) which then moves in a westerly direction. Both reflections reach B at the same time, no matter how fast he is circling. He is only allowed not to change his speed during the course of the experiment.

Every other observer in the universe must observe these unambiguous events in the same way. Nobody reads other times on the clocks than the observer himself. And the arrival of the lightning does not take place in any other place, relative to the environment of the respective observer, than for the observer himself.

We leave out the effects of the length contraction here. It only has an effect on the size of the measured values, but not on the principle effect. First of all, after accelerating, ring B should be lengthened so that it fits parallel to ring A.

No matter how we shield these rings, nothing changes in the result as long as we don't bring other masses into play. Mathematics cannot help us to decide in which ring no centrifugal force is measured, the clocks run fastest and in which ring the lightning bolt reaches the observer from both directions at the same time. Only an actual measurement can help us further. If we lift the curtain, we find that all 3 phenomena are associated with not circling against the universe.

We don't know what is causing these effects, but since we can observe them, see satellite navigation and UTC, there has to be something that corresponds to that. Let's assume there is a field that has exactly these properties and we call it a gravitational field.

The relative relationships resulting from the Lorentz transformations are quite confusing. However, since we can assign the measurements to unambiguous events during the rotation, they are unambiguous and equally valid for all observers.

Let's start with atomic clocks that are set up along the equator and are spatially synchronized with each other according to UTC. By this synchronization, the time that a light signal needs from a clock W from the west to a clock E to the east is measured greater than in the opposite direction.

A clock C moving eastward in relation to the stationary clocks E and W can be seen as being on a faster circling ring; one moving westward than being on a slower circling ring. A clock moving westward has to go faster, and that is exactly what a clock moving westward on earth does.

To get rid of all the irregularities of earth's gravity and atmosphere, let's just imagine the rings again. Starting from the non-circling ring, we take all measurements and thus achieve a host of unambiguous events, such as how the clocks on the other rings behave and how the light signals propagate along the rings. All of these unambiguous measurement results must then also correspond to the measurements of the observers on the circling rings. No calculations should confuse the reader here, only the relative relationships that result from the Lorentz transformations are presented.

Let us now only consider the section between the clocks W and E. They should now be spatially synchronized with one another according to Einstein's definition of simultaneity. Since they were previously synchronized in UTC, the clock E to the east, for example, only needs to be set back by the amount n. Then they measure the speed of light again at the same speed in both directions. The clock E would then lag behind the UTC by the amount n. If we now move a clock C from the clock W to the clock E, or vice versa, then the clock C remains exactly in the spatial simultaneity of these clocks. This corresponds to Einstein's statement that the slow clock transport corresponds to his definition of spatial simultaneity. The displayed value of the clock C at the start compared with the clock W or E differs when it arrives at the other clock E or W only by the amount that results from the Lorentz transformations for this relative movement of C with respect to A and B. So negligible for slow clock transport. The clock C is measured at the same rate as the clocks W and E on its way between the clocks W and E. This measurement result only comes about through the other setting of the measuring instrument for spatial simultaneity. In fact, it goes much slower on the way to the east than results from the Lorentz transformations for the relative movement between the clock C in relation to the clocks W and E, and faster on the way to the west.

The clock C could move at a constant speed in an easterly direction from W to E and further over the rest of the ring back to W. When it came back to W it would then have gone slower by the amount m. On the further way from W to E it no longer seems to go slower compared to W and O, because even when it arrives at E, the displayed value of the clocks of C and E differs by exactly the amount m. The clock C could also change Move west from clock E via clock W and the rest of the ring back to clocks E and W at a constant speed. Then it would have gone faster by the amount m when it arrived at the clock E, and when it arrived at the clock W, the display would also have been different by precisely this amount. It does not matter which part of the ring circumference the distance between W and E makes up. The amount of m is solely dependent on the circumference of the ring and the speed with which the edge moves.

Let's increase the distance between W and E so that it encompasses the entire equator. Then W and E are in the same place. Then W and E could equally determine for all observers that they would have to set different times at a location for spatial synchronization according to Einstein's definition of simultaneity. The difference is exactly m. Only in the non-circling ring are the displayed times of W and E the same. Even with a non-rotating planet, if the clocks were synchronized according to UTC, the time signals at E and W would arrive with the same time difference, i.e. the same time would be measured for both directions.

The clocks W and E are now to be mounted on the circling ring B on a beam that can be rotated in its center. So that the paths of the clocks are the same when turning around relative to the ring, the bar must be rotated in the tangential plane, which corresponds to the horizontal rotation on the earth's surface at the equator. First of all, the clocks should be synchronized with UTC. What effects would be observed if one rotated the bar by 180 °?

1. The clock E moving westward now advances UTC by the value n.

2. The clock W moving eastwards is now lagging behind UTC by the value n.

3. Before turning, the clocks measure a longer time for the light signals from W to E than from E to W.

4. There is no shift in the arrival of the time signals during the rotation.

5. After turning the clocks W and E continue to measure a longer time for the signals from W to E than from E to W. So the other way around than it actually is. Shown even more clearly at the bottom of the text with values ​​for the unique events.

6. Let us carry out a spatial synchronization of the clocks W and E according to Einstein's definition of simultaneity. To do this we have to reset the clock E by the value n. This means that it is behind the UTC by the value n. Now, however, the clocks measure the duration of the time signals in both directions with the same amount.

7. After turning the clock, the clocks W and E continue to measure the duration of the time signals equally in both directions. Now the clock E is again synchronized with the UTC, but the clock W is behind the UTC by the amount n.

Of course, the findings do not only apply to rings the size of the equator. The rings could also correspond to the earth's orbit around the sun or be five times the diameter of the Milky Way. Can be accommodated in a void without any problems without larger masses. If you only consider a small section of the rings in the case of the last-mentioned ring size, the circular movement would hardly be distinguishable from an inertial movement.

Let us imagine a pair of rings the size of the earth's orbit around the sun. In a ring that does not orbit towards the surrounding universe, the atomic clocks would then also go the fastest. Whether the sun is in the center or not would have an effect on the centrifugal force and the gravitational influence on the rate of the clocks, but not on the effects of movement. Inevitably, the clocks that move faster at night due to the rotation of the earth go slower and faster on the day side. The same goes for satellites. The clocks, which move faster in the direction of movement when circling around the earth, must go slower and faster in the opposite direction.

As with the bar that is rotated at the equator, this has no effect on the arrival of the time signals. Therefore, this effect cannot be determined within satellite navigation either. In order to determine this effect, one would actually have to construct a ring of the earth's orbit accordingly and spatially synchronize the clocks in it without contradiction. That would correspond to the principle of UTC, only for the earth's orbit around the sun. At this spatial simultaneity level, the clocks on earth would also go slower at night and faster during the day. Just like a clock moving eastward goes slower and a clock moving westward goes faster.

The real implementation of the Michelson-Morley experiment MME happens while it rotates on earth, circling around the sun and with the sun around the center of the Milky Way. It does not move in an inertial system. Since the rotation of the clocks actually slows down for all observers and the speed of light on the earth's surface is actually not measured at the same speed in both directions, there must also be an actual length contraction, otherwise the MME would not be negative.

Despite all these actual effects, the MME must be negative if the relative ratios correspond to the Lorentz transformations. The Lorentz transformations show that even if we put the MME on rails and accelerate it in an eastward direction to the earth's rotation, or if we slow it down in a westward direction, this would have no effect on the negative output.

If we want to achieve a measurable effect, then we have to reduce the MME to a one-way experiment and place lasers or clocks that work equally constantly at the ends of the arms. Quite possible with the precision of today's atomic clocks. Then a pair of clocks W and E in west-east direction would correspond to one arm of the MME and a pair of clocks N and S in north-south direction would correspond to the other arm. As already described above, rotating such an attempt has no effect. However, if we accelerate this experiment, e.g. in an easterly direction, the time signals arrive at clock E later and later and at clock W earlier and earlier. An acceleration in the opposite direction has exactly the opposite effect. That is why it cannot be seen from this whether the pair of clocks is circling faster or slower after accelerating.

In the case of the pair of clocks N and S lying transversely to the direction of acceleration, there is no effect during acceleration.

Let several pairs of clocks W and E circle past each other at different speeds. According to Einstein's definition of simultaneity, the pairs of clocks that belong together should be spatially synchronized with one another. The measurement results obtained during the passage with mutual observation then also correspond exactly to the predictions of the special theory of relativity during the rotation.

The twin paradox also resolves itself quite logically. From the spatial synchronization of the clock pairs according to Einstein's definition of simultaneity, each clock that moves past is measured as going slower corresponding to the LT. If such a pair of clocks reverses again with the expenditure of energy, then it must, as described above, e.g. set the front clock back by the value x, so that the speed of light is measured equally in both directions again. From the spatial synchronization according to Einstein's definition of simultaneity, a clock moving westwards past you is then measured as going slower, although it actually goes faster.

Time - and what do clocks have to do with it?

We take light clocks as a basis and the atomic clocks that show the same behavior. Depending on their position in relation to the gravitational field, their cycle is different. The second they measure is shorter on the mountain than in the valley. The clocks go faster on the mountain than in the valley.

Pendulum clocks behave in reverse. They are slower on the mountain than in the valley. These clocks are based on a different physical basis. For centuries one could read the time from pendulum clocks. Atomic clocks are more accurate, but do they have more to do with time than pendulum clocks?

A little foray into another area to clarify the question. I want to determine the mass of a body. To do this, I measure the body with a beam balance and a spring balance. I do that again on the moon and get different measurement results with the spring balance. Now I also ask here: What do the measuring instruments have to do with the mass?

I don't want to get too deep into this excursion. Ultimately, different measuring principles (leverage to material expansion) are influenced differently by changes in the environment.

I hope the willing reader will continue to follow me. I think the same goes for any timing instrument. Pendulum clocks show the time just like light clocks.

When measuring the masses with the beam balance, the mass is measured with itself, so to speak. Light clocks measure the movement of light with itself. As a result, light clocks automatically measure the time as it is given in the geometry of the Lorentz transformation, without having to be adjusted.

Light clocks show the time of the special theory of relativity. Atomic clocks behave in the same way. Pendulum clocks do not automatically show the time of the SRT or ART. They have to be re-synchronized depending on the change in the environment in the clock and the display.

But they too depend on the gravitational field and are too imprecise to measure what I intend to do. There should be a physically regular phenomenon, with a frequency and precision similar to atomic clocks, but which is independent of the gravitational field. These clocks would also show the time in Einstein's sense. He said: "Time is something you can read on a clock." But it is not the time of special or general relativity.

Perhaps one has already discovered such a phenomenon, but discarded it because it supposedly does not allow the clocks to run at a constant rate. We want to call such clocks K clocks.

What time values ​​would such a clock show? The measured values ​​that can be achieved with such clocks are quite complicated, as the earth not only rotates, but also orbits the sun. That is why I would first like to leave out the effects that result from the Earth's movement around the sun after the Lorentz transformations and also the gravitational effects of the earth. Let us make a ring in a void orbit with a rotation speed and size corresponding to the equator and we assume it would not move sideways to the gravitational field here.

Let us first place 3 K clocks and 3 atomic clocks next to each other on this ring and synchronize them with each other. The atomic clocks should display the defined second and the K clocks are set accordingly. The atomic clock A(s) stays together with the K clock K(s) stationary on the ring. The atomic clock A(w) together with the K clock K(w) is slowly moved along the ring in a west direction and the atomic clock A(e) together with the K clock K(e) in an east direction. We assume that the clocks are transported slowly, so that the effect of time dilation only plays a subordinate role for the atomic clocks within the ring system.

When the clocks meet again, clocks A(s), K(s), K(w) and K(e) show the same time. The clock A(w) is ahead by the amount m and the clock A(e) is behind by the amount m. The amount m only depends on the circumference of the ring and the tangential speed with which the ring circles. It corresponds to the Sagnac effect.

Development of the formula for calculating m:

To make it clear which value is measured by whom, those from the non-circling ring are supplemented with R and those from the circling ring with K.

The atomic clocks should go according to the defined second.

The lengths are measured with atomic clocks in light seconds Ls. This has the advantage that the measured value for a distance and the time it takes a light signal to cover this distance only differs in terms of seconds and light seconds, but the amount is the same. If we only measure this with one clock, it is easy and a clear value for all observers that corresponds to half the time for the way there and back. If we only measure the one-way route with two clocks, the value depends on the spatial synchronization of the clocks, which does not have to be the same for all observers.

For the way of a time signal, which should correspond to the direction of movement from the circling ring, the path relative to the stationary ring is designated with A and relative to the circling ring with a. For the opposite direction, use B and b accordingly.

The circumference of the stationary ring is denoted by U and the circumference of the moving ring is denoted by u.

U_R = (A_R + B_R) / 2

Since in the stationary ring the lightning components reach the observer from both directions again at the same time, here:

U_R = A_R = B_R

Since the moving ring assumes the same spatial dimensions from the stationary ring: U_R = u_R

Since length contraction occurs in the moving ring, u_K = U_R / root (1 - v² / c²).

The tangential speed with which the rotating ring moves is v and is given in c. Corresponding to the Lorentz transformations, two observers moving towards one another measure the speed of the other at the same rate. So there is no need to distinguish v.

The time aR until the lightning reaches the observer who is moving along the ring in the direction of movement can be calculated as follows:

v * a_R + U_R = y and c * a_R = y So

U_R = c * a_R - v * a_R = (c - v) * a_R So

a_R = U_R / (c - v)                                                                                                                       (1)

For the opposite direction applies:

U_R = c * b_R + v * bR = (c + v) * bR So

bR = UR / (c + v)                                                                                                                     (2)

The time difference mR measured from the stationary ring for the arrival of the lightning components at the circling observer is:

mR = (aR - bR)                                                                                                                        (3)

Taking into account the time dilation, the time difference measured by the circling ring is:

mK = mR * root (1 - v2 / c2)                                                                                                   (4)

This affects the entire ring. To get closer to the length of the beam to be rotated, we first consider the length contraction. The moving ring shortens, creating a gap. Measured from the stationary ring, the length of the moving ring, denoted by bR, is only:

bR_R = U_R * root (1 - v² / c²)                                                                                                      (5)

Due to the resulting gap, the time signals can no longer return to the Moving Observer. So far we have used the ring in both directions, i.e. twice the length of the ring. Now we divide the ring exactly opposite the observer sending the lightning bolt. Therefore we have to halve the times for the light propagation (* 0.5) and thus also the result mR. In principle, nothing else changes.

For the values ​​of this section, n_R and bR_R, and the values ​​of the entire ring, m_R and U_R, there is the relationship:

n_R / (m_R * 0.5) = bR_R / U_R                                           │ we replace bR_R formula (5)

n_R / (m_R * 0.5) = U_R * root (1 - v² / c²) / U_R                 │ we shorten U_R and multiply by (m_R * 0.5)

n_R = (m_R * 0.5) * root (1 - v² / c²)                                                                                         (6)

If we take the time dilation into account, then the time difference n_K measured in the moving ring section corresponds to:

n_K = n_R * root (1 - v² / c²)                                           │ replace nR formula (6)

n_K = m_R * 0.5 * root (1 - v² / c²) * root (1 - v² / c²)      │ replace mR formula (3)

n_K = (a_R - b_R) * 0.5 * (1 - v² / c²)                                 │ replace aR and bR formula (1 + 2)

n_K = (U_R / (c - v) - U_R / (c + v)) * 0.5 * (1 - v² / c²)

The Lorentz transformations show that a body continues to measure itself with the same length even after acceleration. This also corresponds to the relativity principle of the SRT. This means that the length of the accelerated ring section bR_K is measured from the circling ring: bR_K = U_R.

Inserted into the formula:

n_K = (bR_K / (c - v) - bR_K / (c + v)) * 0.5 * (1 - v² / c²)                                                   (7)

These values ​​are all only measured from the circling ring. The length of the bar can be easily determined here and corresponds to half of the time a light signal needs for the way there plus the way back in light seconds. Let us first develop clear events from the point of view of the stationary ring and see how the events open up without contradiction when the bar is turned on the circling ring.

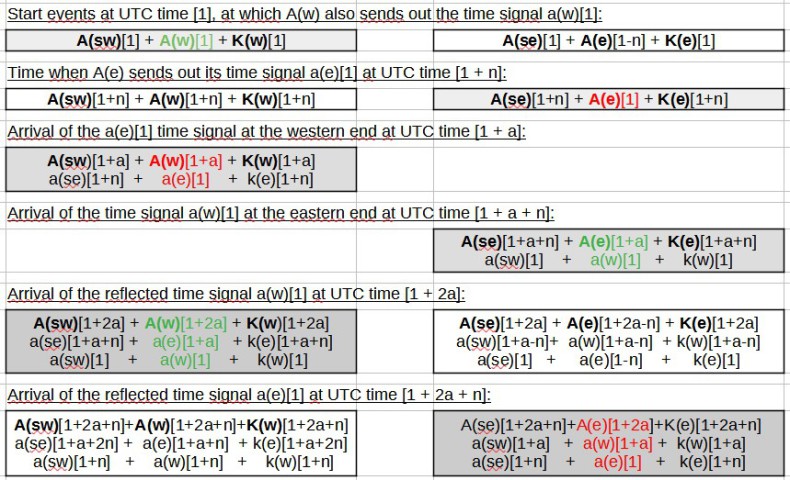
Now we put the clocks A(w) and K(w) together on the west end of a bar and the clocks A(e) and K(e) on the east end. The clocks A(sw) and A(se) should be mounted on the ring at these locations and should remain there when the bar is rotated.

The clocks A(w) and K(w) are together with A(sw) at the same place and therefore also show the same time and their respective time signals 1 spread out with a uniform front. The same applies to clocks A (se), A (e) and K (e) located in the area of ​​the other end of the bar.

The clocks should be spatially synchronized according to UTC. The distance between W and E, measured with their clocks, should be a light seconds.

The time displayed by a clock should, for example, be displayed for clock A(sw) at time 1
as A(sw)[1]. The time signal transmitted at the point in time as a(sw) [1]. The time signals sent out with them by the clocks at their location are added by a +.

So e.g. a(sw)[1] + a(w)[1] + k(w)[1].

The time signals should be reflected at the other end and sent back with the time signals of the clocks located there. The times of the clocks there are also added with + in a new line.

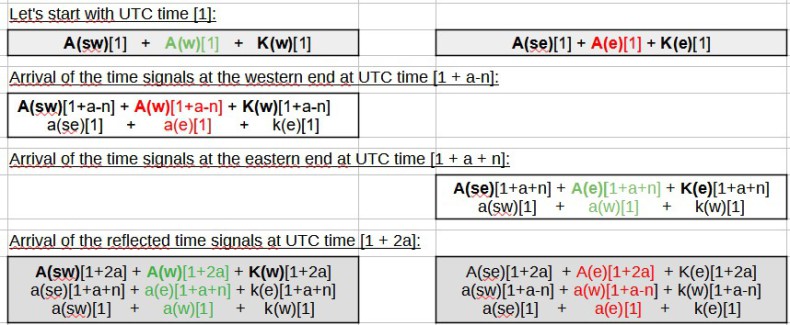
If the clocks A(se) and A(sw) send their time signal 1, then the time signal 1 sent by clock A(se) in a westerly direction arrives at clock A(sw) by 1 + a - n seconds. The time signal sent in an easterly direction by clock A(sw) arrives at clock A(se) by 1 + a + n seconds. The values for a and n are each measured in the proper time of a clock. The clear event at the western end of the bar looks like this when time signal 1 arrives:

The sequence of the unique events is shown in the pictures below. The events related to the time signal a(w)[1] are shown in green. Correspondingly for the time signal a(e)[1] in red. The spatially simultaneous events from the point of view of the clock pair A(w) and A(o) are each highlighted in the sequences with the same shade of gray. The spatially simultaneous events in UTC time are shown next to each other. The time values displayed by the clocks and the movements of the time light signals are calculated from the perspective of the non-rotating ring.

Measured from all clocks, the time signal a(e)[1] needs to the west (a - n) seconds and the time signal a(w)[1] to the east (a + n) seconds. Correspondingly, the times for the way back are reversed.

Now let's turn the bar over. Then the clocks K(w) and K(e) are still synchronized with the clocks

A(sw) and A(se) representing the UTC. However, clock A(w) is n seconds behind UTC because it went slower on the way to the east and clock A(e) is ahead of UTC by n seconds because it went faster on the way to the west. Turning around should take d seconds.

Let us only consider the pair of clocks A(w) and A(e). Before turning around, the time signal [1] of clock A(e), ie a(e)[1], arrives at event A(w)[1+a-n] at A(w) and not halfway through 2a, which would correspond to A(w)[1+a]. The time signal [1] of clock A(w), ie a(w)[1], only arrives at event A(e)[1+a+n] at clock A(e) and not at event A(e)[1+a].

Due to the spatial synchronization of the clocks A(w) and A(e) according to UTC, a longer time is measured for the signal from A(w) to A(e) than vice versa.

Turning it around doesn't change anything. Furthermore, the time signal a(e)[1] arrives at A(w)[1+a-n] and the time signal a(w)[1] at A(e)[1+a+n]. The time signals arrive unchanged at the clocks. The clocks now measure a longer time for the west direction than for the east direction, which is causally incorrect. It only comes about because the clocks A(w) and A(e) are no longer synchronized with UTC. If two lasers, which show a behavior corresponding to the light clocks, send their beams to each other, there would be no shift of the interference pattern while turning.

In order to spatially synchronize clocks A(w) and A(o) with one another according to Einstein's definition of simultaneity, so that they measure the time used by the time signals in both directions with the same amount, we can, for example, clock A(e) by the amount reset n. Then the definite events look like this:

Let us again only consider clocks A(w) and A(e). With this spatial synchronization of the clocks, they measure an equally long time for the duration that the time signals need in both east and west direction, namely half of 2a, i.e. a.

Now we turn the bar around, what should take d seconds.

The clock A(e) went n seconds faster on the way west. It is thus back in sync with UTC, after having previously lagged UTC by n seconds. The clock A(w) has slowed down by n seconds on the way to the east and is now n seconds behind at UTC. Based on this situation, the sequence looks the same as in the previous example. And here, too, the arrival of the time signals does not change when the bar is turned around.

For all observers, the signals for the way there and back need a total of 2a seconds. From the spatial synchronization of clocks A(w) and A(e) according to Einstein's definition of simultaneity, the same time is measured for the east direction as for the westdirection, which does not change when the bar is turned. In the case of rotation, however, this spatial simultaneity is not compatible with the repetitive observations in the sky, the time signals sent over the rest of the ring or the clock transport over the rest of the ring.

This means that the spatial synchronization according to Einstein's definition of simultaneity can be causally refuted as false in the case of rotation by means of unambiguous measurement results.

If one had the possibility to pass on information at a higher speed than the speed of light, then one could narrow the spatial simultaneity more than with light signals. With this, Einstein's definition of simultaneity would also have to be causally refuted as false in the case of linear movement.

If one considers the postulates of the special theory of relativity to be actually given in the universe around us, then there can be none higher than the speed of light. Of course, there can be no WARP drive or wormholes. At least no wormholes that lead back into our universe. Whether I send information at faster than light speed or transport it with a spaceship with a WARP drive makes no difference in causal terms.

Let us assume the situation in which all clocks are synchronized in UTC. After turning the bar, clock A(e) is not only ahead of UTC by n_K seconds, but also ahead of clock K(e). And clock A(w) is not only lagging behind by n_K seconds compared to UTC, but also compared to clock K(w). The time difference n_K that develops between K(w) and A(w) is only dependent on the distance they cover in east-west direction and the tangential speed with which the ring rotates.

What do the results look like if this ring is now mounted on a larger ring C, which corresponds to the earth's orbit around the sun. The UTC clocks are also spatially synchronized accordingly on this ring. Here we want to call the time UTC_S. The time of the clocks stationary on the small ring B we will call UTC_E.

Logically, the clocks on ring B behave like the clocks on the bar in the previous example, which you just keep turning. Here, too, the clocks in the UTC_E go slower than the clocks in the UTC_S when moving in the direction of the earth's movement and faster in the opposite direction. As with turning the bar, however, this has no influence on the arrival of the time signals within ring B, provided that the sending and receiving times are measured with light or atomic clocks.

Since the K-clocks do not behave according to the Lorentz transformations, a time difference with a sinusoidal change arises between the atomic clocks and the K-clocks standing next to them. Instead, they show a behavior corresponding to the bar example, i.e. no change to the clocks of the UTC_S.

However, the earth's orbit circles with the sun around the center of the Milky Way. If our example is expanded to include a corresponding effect, there will be a sinusoidally fluctuating time difference between the K-clocks and the UTC_S. This would superimpose the curve of the time difference between the UTC_E and the K clocks. So we would only have a comparable curve for the fluctuation of the time difference after one year at the earliest.

Is there a difference between the measured values that can be achieved with atomic clocks in inertial systems or turning cylinders?

Let us consider only a section of a cylinder surface (cylinder diameter three times the Milky Way diameter) with the edge length of one astronomical unit. In this section, the clocks are spatially synchronized according to Einstein's definition of simultaneity. Under these conditions, the clock rate and the propagation of light signals are as in an inertial system. If we let two or more cylinder surfaces move past each other and only look at the atomic clocks and time light signals, then the measurement results and calculations correspond exactly to the relationships of inertial systems. But we could still send signals along the cylinder, even if that would take a few millions of years. This would enable us to generate measurements that would causally represent the spatial synchronization of the clocks according to Einstein's definition of simultaneity as incorrect.

Only when we detach this surface from the cylinder do we actually have a straight-line movement, even if this hardly differs measurably from the other movement. With that the centrifugal force is gone. It is also questionable whether a time signal that we send through the universe in one direction would reach us again from the other direction. But we can still see the universe go by. However, there are no repetitive observations in the sky.

Isolated theoretical considerations have a particular flaw. They have no relation to the reality around us. Let us consider 2 spacemen who move in a straight line past each other at half the speed of light. According to the SRT, they should have equal rights. But what about when we do that in reality?

One is still on Spaceship Earth. He sees a universe around him that looks about the same in all directions. About the same radiation reaches it from all directions. In this universe he sees the other spaceman moving past him at half the speed of light.

The other spaceman also sees him passing at half the speed of light, but with him he sees a whole universe passing by. This also does not look the same in all directions. In one direction it is redshifted. He receives very little low-energy radiation from this direction. In the other direction it is blue-shifted. Massive high-energy radiation acts on him from this direction. This radiation must inevitably accelerate his spaceship in the direction of the movement of the universe. It should also be possible to measure this with sensitive measuring instruments inside the spaceship.

Even if the situation is a little different, we can already measure so precisely today that the Pioneer anomaly could be detected. The cause was only a very small difference in the calculation of the energy received and the energy emitted. The difference in radiation acting on the spaceman should be significantly greater.

Can one really consider both astronauts to have equal rights here, just because they are both theoretically and mathematically in an inertial system when viewed in isolation?

Who can take the big step with me and question the absolute constancy of the speed of light and assume it is constant to the gravitational field?

Who can still assume that the gravitational field, formed from the overlapping fields of the mass particles, would be a plastically deformable field in its effect? Then the Mercury anomaly and the Schiff effect could not only be superimpositions of the gravitational field, as Einstein interpreted it, but plastic changes in the field. This would also mean that the earth deforms the gravitational field slightly on its way around the sun and takes it with it, which causes the fly-by anomaly. The effect could be even greater if the masses that locally determine the gravitational field move in a common direction. The gravitational field causes the centrifugal force. But if this rotates a bit with rotating galaxies, it looks from the outside as if the stars are moving too fast. But it is exactly the right speed for the prevailing gravitational field, even without dark matter.

I would consider that the simpler solution and therefore the right one after Ockham’s razor.

Which mathematician with access to the astronomical data might consider this solution?