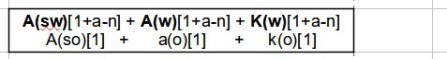2021SMuK

    Title: Methode um die Bewegung zum Gravitationsfeld zu messen.

    Authors: Karl-Herbert Darmer

    Day, time, and location: Wed, Sep 1 2021, 15:00-15:15, H6

    Session number: GR 5.5

    Serial number: GR 40

Ich habe den Vortrag hier dargestellt, da er für 10 Minuten zu umfangreich ist und so komprimiert kaum verständlich dargestellt werden kann. Im Vortrag selbst werde ich mich auf die prinzipiellen Ideen beschränken und die Schlussfolgerungen etwas ausführlicher darstellen.

Eine Methode um die lineare Bewegung zum Gravitationsfeld zu messen.

Haben wir die Relativität schon richtig verstanden? Die Dunkle Materie lässt sich genauso schlecht fassen, wie vor mehr als 100 Jahren die Eigenschaften des Äthers. Vielleicht hat man während der Corona-Pandemie Zeit die Dogmen im Sinne Einsteins in Frage zu stellen. Im Sinne Einsteins heißt, dass man das was man gerade aktuell für richtig hält in Frage stellt. Dabei darf man aber nicht die Frage auf Gleise setzen, die genau zu dem Ergebnis führen, das die Dogmen bestätigt.

Ganz zu Anfang möchte ich die Frage stellen: Ist der leere Raum wirklich leer?

Um die Frage zu verdeutlichen: Stellen wir uns zwei gleichgroße Ringe parallel nebeneinander vor. Um möglichst wenig Masse zu verwenden sollen es nur dünne Ringgerüste sein, entfernt von anderen Massen in einem Void. Am Rand der Ringe sitzen Beobachter. Die Ringe drehen sich zueinander um ihre gemeinsame Achse. In dem einen Ring wird keine Zentrifugalkraft gemessen. Aus der Größe der Ringe und der Winkelgeschwindigkeit lässt sich die Zentrifugalkraft berechnen, die am Rand des anderen Kreisels gemessen werden sollte.

Aber muss hier wirklich eine Zentrifugalkraft gemessen werden und wenn ja, was bestimmt die Größe? Bestimmt das die Mathematik, oder ist hier etwas im leeren Raum vorhanden, das die Zentrifugalkraft hervorbringt und damit auch die Größe bestimmt?

Unabhängig von Mathematik oder menschlicher Vorstellung: Bei einer realen Durchführung des Versuchs wird am Rand des Rings keine Zentrifugalkraft gemessen, der zum umliegenden Universum nicht rotiert. In dem dazu rotierenden Ring wird eine Zentrifugalkraft gemessen.

Stellen wir uns einen Ring vor, der so schnell rotiert, dass sein Rand sich gegenüber einem nicht rotierenden Ring mit halber Licht­geschwindig­keit bewegt. Damit bewegt sich der auf dem Rand sitzende Beobachter mit halber Licht­geschwindig­keit zum Gravitationsfeld. Jetzt löst er sich vom Ring. Damit bewegt er sich tangential auf geradliniger Bahn von dem Ring weg. Das entspricht einer inertialen Bewegung. Nach der Speziellen Relativitäts­theorie kann er sich jetzt nicht mehr zu Gravitationsfeld bewegen, denn dann könnte er auch dazu ruhen und es gäbe einen bevorzugten Ruhezustand. Ich möchte an dieser Stelle nicht genauer darauf eingehen. Mit der nachfolgend dargestellten Methode kann man bei der Rotation die Bewegung zum Gravitationsfeld messen und damit auch den Ruhezustand bestimmen. Das muss dann auch für die geradlinige Bewegung gelten.

Meine Frage lautet: Ist der leere Raum wirklich leer, oder gibt es ein Gravitationsfeld, zu dem man sich dann auch geradlinig bewegen kann?

Um uns der Antwort zu nähern, soll hier ein Weg gezeigt werden, der nur auf eindeutigen Ereignissen aufbaut, die für jeden Beobachter gelten müssen, egal wie sie sich bewegen oder wo sie sich aufhalten.

Als eindeutige Ereignisse wird die Begegnung zweier Beobachter A und B mit ihren Uhren gesehen. Bei dieser Begegnung vergleichen sie ihre Uhren. Die dabei angezeigten Uhrenwerte gelten für alle Beobachter. Auch die Informationen, die sie in diesem Moment aus dem Weltraum erhalten, sind für alle anderen Beobachter genau in diesem Moment eingetroffen.

Auch die Kausalität ist für alle Beobachter eindeutig, denn alles was A und B danach erleben ist auch für alle anderen danach geschehen und alles was A und B davor erlebt haben ist auch für alle anderen davor geschehen. Die Abfolge der Ereignisse ist für alle gleich. Das ist die Grundlage für die Idee der Weltlinien. Wie andere Beobachter diese Ereignisse zu ihrer Eigenzeit einordnen, und wie groß sie die Entfernung zu diesen Ereignissen, oder die Entfernung solcher Ereignisse zueinander messen, hängt von der Einstellung der Messinstrumente für die räumliche Gleichzeitigkeit ab. Diese kann für alle Beobachter unterschiedlich sein, da es hierfür bisher keine Möglichkeit gibt sie eindeutig zu bestimmen.

Die relativen Verhältnisse der Messergebnisse, mit Atomuhren und Lichtsignalen unter Einsteins Gleich­zeitigkeits­definition gemessen, entsprechen in dem uns umgebenden Universum unzweifelhaft den Lorentztransformationen. Bisher konnten jedenfalls keine dem widersprechenden Beobachtungen gemacht werden. Mathematische Formeln sind schwer zu verstehen. Noch schwerer ist zu erkennen welche Konsequenzen sich daraus ergeben.

Ausgehend von einem Beobachter sollen eindeutige Ereignisse errechnet werden. Diese muss dann auch jeder dazu bewegte Beobachter in seinen Messungen unterbringen, ohne dass dabei Widersprüche auftreten.

Kommen wir wieder zu dem Versuch zweier parallel nebeneinander kreisender Ringe, weit ab von größeren Massen. Am Rand des einen Rings wird keine Zentrifugalkraft gemessen. Diesen Zustand wollen wir als nicht kreisen bezeichnen.

Übertragen wir die Erkenntnisse, die wir aus der Satellitennavigation und der Universal Time Coordinated UTC gewonnen haben, auf diesen Versuch.

Zum Messen der Zeit verwenden wir den Lichtuhren entsprechende Atomuhren. Räumliche Distanzen wollen wir zunächst nicht messen. Bei Bewegung räumlich entfernter Messpunkte ist der Messwert von der räumlichen Gleichzeitigkeit abhängig. Diese kann kausal immer nur im Rahmen der Weltlinie der schnellsten Weitergabemöglichkeit für Informationen eingegrenzt werden, aber nicht eindeutig bestimmt werden.
Hier ein kleiner Ausflug für in der Materie Unerfahrene:

Eine Information wird ausgesendet, sie wird an einem entfernten Ort beantwortet und wieder empfangen. Kausal kann das Beantworten nur nach dem Aussenden und vor dem wieder Empfangen geschehen sein. Wann genau sie innerhalb dieser Zeitspanne geschehen ist kann man nicht bestimmen.

Die Information könnte erst mit der Post geschickt worden sein, was einen Tag dauert und dann als Telegramm, was nur eine halbe Stunde dauert. Es könnte aber auch anders herum sein. Um eingrenzen zu können, wann die Beantwortung geschehen sein könnte muss man etwas über den Transport der Information wissen.

Nehmen wir ein Schallsignal und lassen es als Antwort einfach reflektieren, wie in den Bergen ein Echo. Wann hat dann die Reflektion stattgefunden. Genau zur Hälfte der Zeit für Hin- und Rückweg? Wenn etwas Wind weht, hat das Schallsignal in Richtung des Windes weniger Zeit gebraucht, als in der Gegenrichtung. Auch hier ist der Zeitpunkt nicht sicher einzugrenzen.

Wie steht es mit Licht. Nehmen wir ein Lichtsignal. Es ist das schnellste was wir zur Verfügung haben. Als Antwort lassen wir auch dieses einfach reflektieren. Aber auch das ist keine eindeutige Lösung. Wie wir in dem später dargestellten Beispiel erkennen können ist die Geschwindigkeitsmessung einer Bewegung abhängig von der Einstellung der räumlichen Gleichzeitigkeit. Werden nur Lichtuhren und Lichtsignale verwendet und jeder Beobachter stellt seine Messinstrumente für die räumliche Gleichzeitigkeit so ein, dass sie Einsteins Gleich­zeitigkeits­definition entsprechen, dann gehen die Ergebnisse immer für alle Beobachter ineinander auf. Wie später gezeigt wird gilt das auch vollständig für die Rotation.

Zurück zu den Ringen. Positionieren wir auf dem nicht kreisenden Ring A die Atomuhr A bei dem Beobachter A. Auf dem dazu im Sinne der Erddrehung nach Osten kreisenden Ring B die Atomuhr B bei dem Beobachter B.

Die Atomuhren sollen die Zeit entsprechend der definierten Sekunde anzeigen. Dann ist die Uhr B bei jeder Begegnung mit A langsamer gegangen. Auf allen Uhren, die auf kreisenden Ringen positioniert sind vergehen die Sekunden langsamer. Um so schneller sie kreisen, um so langsamer gehen die Uhren. Die Begegnungen der Uhren sind eindeutige Ereignisse. Daraus Folgt, dass auch für Beobachter B seine Uhr B langsamer geht als die Uhr A.

Jetzt senden A und B bei ihrer Begegnung einen Lichtblitz aus, der sich entlang der Ringe in beide Richtungen ausbreiten soll. Dann erreichen nur bei dem nicht kreisenden Ring A die sich entgegengesetzt bewegenden Blitzanteile den Beobachter A aus beiden Richtungen gleichzeitig. Licht breitet sich mit einer einheitlichen Front aus. Im Universum wurde bisher nichts anderes beobachtet. Dann können die Blitzanteile den zu A bewegten B nicht aus beiden Richtungen gleichzeitig erreichen. Der sich in Westrichtung ausbreitende Blitzanteil, also entgegen der Bewegungsrichtung von B, erreicht ihn zuerst und dann erst der sich in Ostrichtung ausbreitende Blitzanteil. Das entspricht auch den Erkenntnissen aus der Satellitennavigation.

Die Beobachter sollen die Blitzanteile reflektieren, wenn sie von diesen erreicht werden. A erzeugt dadurch für alle Beobachter gleichzeitig die Reflexionen A(ow) und A(wo). Diese erreichen für alle Beobachter A auch wieder gleichzeitig.

B erzeugt dabei zuerst die Reflexionen B(wo), von dem Blitzanteil, der sich anfangs in Westrichtung ausgebreitet hat und nach der Reflexion sich in Ostrichtung bewegt. Erst etwas später erreicht ihn der Blitzanteil, der sich in Ostrichtung bewegt hat. Mit diesem erzeugt er die Reflexion B(ow) die sich dann in Westrichtung bewegt. Diese Reflexionen erreichen B gleichzeitig, egal wie schnell er kreist. Er darf nur während des Versuchsablaufs seine Geschwindigkeit nicht verändern.

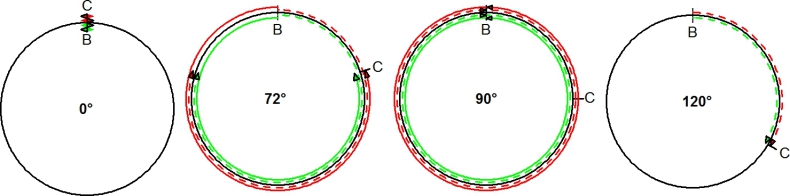
Der Äquator vom Südpol aus betrachtet. C bewegt sich mit einem Viertel der Lichtgeschwindigkeit. Die durchgezogenen Linien stellen die von B und C in Westrichtung ausgesendeten Lichtblitze dar. Die gestrichelten Linien die in Ostrichtung ausgebreiteten Lichtblitze.Hätte C die Lichtblitze jeweils reflektiert, würden ihn beide Reflexionen gleichzeitig bei 192° erreichen.

Diese eindeutigen Ereignisse muss auch jeder andere Beobachter im Universum so beobachten. Keiner liest auf den Uhren andere Zeiten ab, als die Beobachter selbst. Und das Eintreffen der Blitze findet an keinem anderen Ort statt, relativ zur Umgebung der jeweiligen Beobachter, als für den Beobachter selbst.

Die Effekte der Längenkontraktion lassen wir hier außen vor. Sie hat nur einen Effekt auf die Größe der Messwerte, aber nicht auf den prinzipiellen Effekt. Zunächst soll der Ring B nach dem Beschleunigen jeweils so verlängert werden, dass er parallel neben den Ring A passt.

Egal wie wir diese Ringe abschirmen, es ändert sich nichts an dem Ergebnis, solange wir keine anderen Massen ins Spiel bringen. Die Mathematik kann uns nicht helfen zu entscheiden in welchem Ring keine Zentrifugalkraft gemessen wird, die Uhren am schnellsten gehen und in welchem Ring der Blitz den Beobachter aus beiden Richtungen gleichzeitig erreicht. Nur eine tatsächliche Messung kann uns da weiter helfen. Lichten wir den Vorhang, dann stellen wir fest, dass alle 3 Phänomene mit einem nicht Kreisen gegenüber dem uns umgebenden Universum einhergehen.

Wir wissen nicht was diese Effekte hervorbringt, aber da wir sie beobachten können, siehe Satellitennavigation und UTC, muss es etwas geben, das dem entspricht. Nehmen wir an es gibt ein Feld, dass genau diese Eigenschaften hat und nennen es Gravitationsfeld.

Die relativen Verhältnisse die sich aus den Lorentztransformationen ergeben sind durchaus verwirrend. Da wir bei der Rotation aber die Messungen eindeutigen Ereignissen zuordnen können, sind sie eindeutig und für alle Beobachter gleichermaßen gültig.

Beginnen wir mit Atomuhren die entlang des Äquators aufgestellt werden und entsprechend der UTC räumlich miteinander synchronisiert werden. Aus dieser Synchronisation heraus wird die Zeit, die ein Lichtsignal von einer westlich gelegene Uhr W zu einer östlich gelegenen Uhr O braucht, als größer gemessen, als in der entgegengesetzten Richtung.

Eine gegenüber den stationären Uhren O und W ostwärts bewegte Uhr C können wir als auf einem schneller kreisenden Ring befindlich ansehen; eine westwärts bewegte als auf einem langsamer kreisenden Ring befindlich. Eine westwärts bewegte Uhr muss also schneller gehen, und genau das macht eine auf der Erde westwärts bewegte Uhr.

Um die ganzen Unregelmäßigkeiten der Erdgravitation und der Atmosphäre weg zu lassen, stellen wir uns wieder nur die Ringe vor. Ausgehend von dem nicht kreisenden Ring nehmen wir alle Messungen vor und erzielen damit eine Schar eindeutiger Ereignisse, wie sich die Uhren auf den anderen Ringen verhalten und wie sich die Lichtsignale entlang der Ringe ausbreiten. All diese eindeutigen Messergebnisse müssen dann auch den Messungen der Beobachter auf den kreisenden Ringen entsprechen. Hier sollen keine Rechnungen den Leser verwirren sondern nur die relativen Verhältnisse dargestellt werden, die sich aus den Lorentz­transformationen ergeben.

Betrachten wir jetzt nur das Teilstück zwischen den Uhren W und O. Sie sollen jetzt räumlich nach Einsteins Gleichzeitigkeitsdefinition miteinander synchronisiert werden. Da sie vorher in der UTC synchron waren, braucht dazu z.B. die östlich gelegene Uhr O nur um den Betrag n zurück gestellt werden. Dann messen sie die Lichtgeschwindigkeit wieder in beiden Richtungen gleich schnell. Die Uhr O würde dann aber gegenüber der UTC um den Betrag n nachgehen. Bewegen wir nun eine Uhr C von der westlich gelegenen Uhr W zur Uhr O, oder umgekehrt, dann bleibt die Uhr C genau in der räumlichen Gleichzeitigkeit dieser Uhren. Das entspricht Einsteins Aussage, dass der langsame Uhrentransport seiner räumlichen Gleichzeitigkeitsdefinition entspricht. Der angezeigte Wert der Uhr C beim Start mit der Uhr W oder O abgeglichen, unterscheidet sich beim Eintreffen bei der anderen Uhr O oder W nur um den Betrag, der sich aus den Lorentz­transformationen für diese Relativbewegung von C gegenüber A und B ergibt. Bei einem langsamen Uhrentransport also zu vernachlässigen. Die Uhr C wird auf ihrem Weg zwischen den Uhren W und O als gleich schnell gehend mit den Uhren W und O gemessen. Dieses Messergebnis kommt nur durch die andere Einstellung des Messinstruments für die räumliche Gleichzeitigkeit zustande. Tatsächlich geht sie auf dem Weg nach Osten viel langsamer, als sich aus den Lorentz­transformationen für die Relativbewegung zwischen der Uhr C gegenüber den Uhren W und O ergibt und auf dem Weg nach Westen schneller.

Die Uhr C könnte sich mit gleichbleibender Geschwindigkeit in Ostrichtung von W nach O und weiter über den Rest des Ringes wieder zu W bewegen. Beim Wiedereintreffen bei W wäre sie dann um den Betrag m langsamer gegangen. Auf dem weiteren Weg von W nach O scheint sie gegenüber W und O nicht mehr langsamer zu gehen, denn auch bei Eintreffen bei O unterscheidet sich der angezeigte Wert der Uhren von C und O genau um den Betrag m. Die Uhr C könnte sich auch mit gleichbleibender Geschwindigkeit in Westrichtung von der Uhr O über die Uhr W und den Rest des Rings wieder zu den Uhren O und W bewegen. Dann wäre sie beim Eintreffen bei der Uhr O um den Betrag m schneller gegangen als diese und auch beim Eintreffen bei der Uhr W unterscheidet sich die Anzeige genau um diesen Betrag. Dabei ist egal welchen Anteil des Ringumfangs der Abstand zwischen W und O ausmacht. Der Betrag von m ist allein abhängig von dem Umfang des Ringes und der Geschwindigkeit mit der er sich bewegt.

Vergrößern wir den Abstand zwischen W und O, so dass er den gesamten Äquator umfasst. Dann befinden sich W und O am selben Ort. Dann könnten W und O für alle Beobachter gleichermaßen feststellen, dass sie für eine räumliche Synchronisation nach Einsteins Gleichzeitigkeitsdefinition an einem Ort unterschiedliche Zeiten einstellen müssten. Die Differenz beträgt genau m. Nur in dem nicht kreisenden Ring sind die angezeigten Uhrzeiten von W und O gleich. Auch nur bei einem nicht rotierenden Planeten würden bei einer der UTC entsprechenden Synchronisation der Uhren die Zeitsignale bei O und W mit der gleichen Zeitdifferenz eintreffen, also für beide Richtungen eine gleichlange Zeit gemessen werden.

Die Uhren W und O sollen jetzt auf dem kreisenden Ring B auf einem Balken montiert werden, der in seiner Mitte gedreht werden kann. Damit die Wege der Uhren beim Umdrehen relativ zum Ring gleich sind, muss der Balken in der Tangentialebene gedreht werden, was dem waagerechten Drehen auf der Erdoberfläche am Äquator entspricht. Zunächst sollen die Uhren mit der UTC synchron sein. Welche Effekte wären zu beobachten, wenn man den Balken um 180° dreht?

1. Die westwärts bewegte Uhr O geht jetzt um den Wert n gegenüber der UTC vor.

2. Die ostwärts bewegte Uhr W geht jetzt um den Wert n gegenüber der UTC nach.

3.Die Uhren messen vor dem Umdrehen eine längere Zeit für die Lichtsignale von W nach O als von O nach W.

4. Während des Umdrehens kommt es zu keiner Verschiebung des Eintreffens der Zeitsignale.

5. Nach dem Umdrehen messen die Uhren W und O weiterhin eine längere Zeit für die Signale von W nach O als von O nach W. Also umgekehrt als es tatsächlich ist. Unten im Text noch deutlicher dargestellt mit Werten für die eindeutigen Ereignisse.

6. Nehmen wir eine räumliche Synchronisation der Uhren W und O nach Einsteins Gleich­zeitigkeits­definition vor. Dazu müssen wir z. B. die Uhr O um den Wert n zurückstellen. Damit geht sie gegenüber der UTC um den Wert n nach. Jetzt messen die Uhren aber die Zeitdauer für die Zeitsignale in beiden Richtungen gleich groß.

7. Nach dem Umdrehen messen die Uhren W und O die Zeitdauer für die Zeitsignale weiterhin in beiden Richtungen gleich groß. Jetzt ist die Uhr O wieder synchron mit der UTC, dafür geht die Uhr W um den Betrag n gegenüber der UTC nach.

Die Feststellungen gelten natürlich nicht nur für Ringe mit der Größe des Äquators. Die Ringe könnten auch der Erdbahn um die Sonne entsprechen oder den fünffachen Durchmesser der Milchstraße haben. In einem Void problemlos unterzubringen, ohne dass größere Massen stören. Betrachtet man bei der letztgenannten Ringgröße nur einen kleinen Teilabschnitt der Ringe, wäre die kreisende Bewegung kaum noch unterscheidbar von einer inertialen Bewegung.

Stellen wir uns ein Ringpaar in der Größe der Erdbahn um die Sonne vor. In einem zum umliegenden Universum nicht kreisenden Ring würden dann die Atomuhren auch am schnellsten gehen. Ob die Sonne im Zentrum vorhanden ist oder nicht, hätte einen Effekt auf die Zentrifugalkraft und den gravitativen Einfluss auf den Gang der Uhren, nicht aber auf die Bewegungseffekte. Zwangsläufig gehen die hier durch das Rotieren der Erde nachts schneller bewegten Uhren langsamer und und auf der Tagseite schneller. Das gleiche gilt für Satelliten. Die sich beim Kreisen um die Erde in Bewegungsrichtung schneller bewegenden Uhren müssen langsamer und in entgegengesetzter Richtung schneller gehen.

Wie bei dem Balken, der am Äquator gedreht wird, hat das aber keinen Effekt auf das Eintreffen der Zeitsignale. Deshalb kann dieser Effekt auch innerhalb der Satellitennavigation nicht festgestellt werden. Um diesen Effekt festzustellen, müsste man tatsächlich einen Ring der Erdbahn entsprechend konstruieren und in diesem die Uhren widerspruchsfrei räumlich synchronisieren. Das würde dem Prinzip der UTC entsprechen, nur eben für die Erdbahn um die Sonne. Zu dieser räumlichen Gleichzeitigkeitsebene würden die Uhren auf der Erde auch nachts langsamer und tags schneller gehen. So wie eine ostwärts bewegte Uhr langsamer und eine westwärts bewegte Uhr schneller geht.

Die reale Durchführung des Michelson-Morley-Experiments MME geschieht während es auf der Erde mitrotiert, kreisend um die Sonne und mit der Sonne um das Milchstraßen­zentrum. Es bewegt sich nicht in einem Inertialsystem. Da es bei der Rotation für alle Beobachter zu einer tatsächlichen Verlangsamung der Uhren kommt und die Lichtgeschwindigkeit auf der Erdoberfläche tatsächlich nicht in beiden Richtungen gleich schnell gemessen wird, muss es auch zu einer tatsächlichen Längenkontraktion kommen, sonst würde das MME nicht negativ ausfallen.

Trotz all dieser tatsächlichen Effekte muss das MME negativ ausfallen, wenn die relativen Verhältnisse den Lorentz­transformationen entsprechen. Aus den Lorentz­transformationen geht hervor, auch wenn wir das MME auf Gleise stellen und es in Ostrichtung zur Erdrotation beschleunigen, oder in Westrichtung verlangsamen hätte das keinen Effekt auf den negativen Ausgang.

Wenn wir einen messbaren Effekt erzielen wollen, dann müssen wir das MME auf ein Einweg-Experiment reduzieren und an die Enden der Arme jeweils gleich konstant arbeitende Laser oder Uhren stellen. Bei der Präzision heutiger Atomuhren durchaus möglich. Dann entspräche ein Uhrenpaar W und O in West-Ost Richtung dem einen Arm des MME und ein Uhrenpaar N und S in Nord-Süd Richtung dem anderen Arm. Wie schon oben beschrieben, hat das Drehen eines solchen Versuchs keinen Effekt. Wenn wir diesen Versuch aber z.B. in Ostrichtung beschleunigen, treffen die Zeitsignale bei der Uhr O immer später und bei der Uhr W immer früher ein. Eine Beschleunigung in umgekehrter Richtung hat genau den umgekehrten Effekt. Deshalb lässt sich daraus auch nicht erkennen, ob das Uhrenpaar nach dem Beschleunigen schneller oder langsamer kreist.

Bei dem zur Beschleunigungsrichtung quer liegenden Uhrenpaar N und S kommt es bei der Beschleunigung zu keinem Effekt.

Lassen wir mehrere Uhrenpaare W und O mit unterschiedlicher Geschwindigkeit aneinander vorbei kreisen. Die zusammen gehörenden Uhrenpaare sollen jeweils nach Einsteins Gleich­zeitigkeits­definition räumlich miteinander synchronisiert sein. Die bei der Passage bei gegenseitiger Beobachtung erzielten Messergebnisse entsprechen dann auch bei der Rotation exakt den Vorhersagen der Speziellen Relativitäts­theorie.

Auch das Zwillingsparadoxon löst sich ganz logisch. Aus der räumlichen Synchronisation der Uhrenpaare nach Einsteins Gleich­zeitigkeits­definition heraus wird jede daran vorbei bewegte Uhr als den LT entsprechend langsamer gehend gemessen. Kehrt ein solches Uhrenpaar unter Energieaufwand wieder um, dann muss es wie oben beschrieben z.B, die vordere Uhr um den Wert x zurückstellen, damit die Licht­geschwindig­keit wieder in beiden Richtungen gleich groß gemessen wird. Aus der räumlichen Synchronisation nach Einsteins Gleich­zeitigkeits­definition heraus wird dann auch eine westwärts an ihnen vorbeiziehende Uhr als langsamer gehend gemessen, obwohl sie tatsächlich schneller geht.

Die Zeit - und was haben Uhren damit zu tun?

Wir nehmen als Basis Lichtuhren und die ein gleiches Verhalten zeigenden Atomuhren. Abhängig von ihrer Lage zum Gravitationsfeld gehen sie dann unterschiedlich schnell. Die von ihnen gemessene Sekunde ist auf dem Berg kürzer als im Tal. Sie gehen damit auf dem Berg schneller als im Tal.

Pendeluhren haben ein umgekehrtes Verhalten. Sie sind auf dem Berg langsamer als im Tal. Ihr Taktgeber beruht auf einer anderen physikalischen Basis. Jahrhunderte konnte man von Pendeluhren die Zeit ablesen. Atomuhren sind genauer, aber haben sie mehr mit der Zeit zu tun als Pendeluhren?

Ein kleiner Ausflug auf ein anderes Gebiet, um die Frage zu verdeutlichen. Ich möchte die Masse eines Körpers bestimmen. Dazu messe ich den Körper mit einer Balkenwaage und mit einer Federwaage. Das mache ich auch noch einmal auf dem Mond und erhalte mit der Federwaage unterschiedliche Messergebnisse. Jetzt frage ich auch hier: Was haben die Messinstrumente mit der Masse zu tun?

Ich möchte nicht zu tief in diesen Ausflug einsteigen. Letztendlich werden unterschiedliche Messprinzipien (Hebelwirkung zu Materialdehnung) durch Umgebungsveränderungen unterschiedlich beeinflusst.

Ich hoffe, dass der willige Leser mir weiter folgen wird. Ich denke das gleiche gilt für jedes Zeitmessinstrument. Pendeluhren zeigen genauso die Zeit an, wie Lichtuhren.

Bei dem Messen der Massen mit der Balkenwaage wird die Masse sozusagen mit sich selbst gemessen. Mit Lichtuhren wird die Lichtbewegung mit sich selbst gemessen. Dadurch messen Lichtuhren die Zeit automatisch so, wie sie in der Geometrie der Lorentz­transformationen gegeben ist, ohne dass sie verstellt werden müssen.

Lichtuhren zeigen die Zeit der Speziellen Relativitäts­theorie an. Atomuhren haben ein gleiches Verhalten. Pendeluhren zeigen nicht automatisch die Zeit der SRT oder ART an. Sie müssen je nach Umgebungsveränderung im Takt und der Anzeige neu synchronisiert werden.

Aber auch sie hängen vom Gravitationsfeld ab und gehen zu ungenau, um das zu messen, was ich beabsichtige. Es müsste ein physikalisch regelmäßiges Phänomen geben, mit einer ähnlichen Frequenz und Präzision wie Atomuhren, das aber unabhängig ist vom Gravitationsfeld. Auch diese Uhren würden die Zeit im Sinne Einsteins anzeigen. Er sagte: „Die Zeit ist etwas, was man von einer Uhr ablesen kann.“ Es ist aber nicht die Zeit der Speziellen oder Allgemeinen Relativitäts­theorie.

Vielleicht hat man schon ein solches Phänomen entdeckt, aber wieder verworfen, weil man damit vermeintlich keinen konstanten Gang der Uhren zustande bekommt. Solche Uhren wollen wir K-Uhren nennen.

Welche Zeitwerte würde eine solche Uhr anzeigen? Die mit solchen Uhren erzielbaren Messwerte sind recht kompliziert, da sich die Erde nicht nur dreht, sondern auch um die Sonne kreist. Darum möchte ich zunächst die Effekte weglassen, die sich nach den Lorentz­transformationen aus der Erdbewegung um die Sonne ergeben und auch die gravitativen Effekte der Erde. Lassen wir einen Ring in einem Void kreisen mit einer dem Äquator entsprechenden Geschwindigkeit und Größe und wir nehmen an er würde sich hier nicht zum Gravitationsfeld seitwärts bewegen.

Stellen wir auf diesem Ring zunächst 3 K-Uhren und 3 Atomuhren nebeneinander und synchronisieren sie miteinander. Die Atomuhren sollen die definierte Sekunde anzeigen und die K Uhren werden entsprechend eingestellt. Die Atomuhr A(s) bleibt zusammen mit der K-Uhr K(s) stehen. Die Atomuhr A(w) wird zusammen mit der K-Uhr K(w) langsam entlang des Rings in Westrichtung bewegt und die Atomuhr A(o) zusammen mit der K-Uhr K(o) in Ostrichtung. Wir gehen davon aus, dass die Uhren langsam transportiert werden, so das der Effekt der Zeitdilatation für die Atomuhren innerhalb des Ringsystems nur eine untergeordnete Rolle Spielt.

Treffen die Uhren wieder zusammen, dann zeigen die Uhren A(s), K(s), K(w) und K(o) die gleiche Zeit an. Die Uhr A(w) geht um den Betrag m vor und die Uhr A(o) geht um den Betrag m nach. Der Betrag m ist nur abhängig von dem Umfang des Rings und der Tangentialgeschwindigkeit mit der der Ring kreist. Er entspricht dem Sagnac-Effekt.

Entwicklung der Formel zur Berechnung m:

Um deutlich zu machen welcher Wert von wem gemessen wird, werden die vom nicht Kreisenden Ring mit R ergänzt und die vom kreisenden Ring mit K ergänzt.

Die Atomuhren sollen der definierten Sekunde entsprechend gehen.

Die Längen werden mit Atomuhren in Lichtsekunden Ls gemessen. Das hat den Vorteil, dass sich der Messwert für eine Entfernung und die Zeit, die ein Lichtsignal braucht um diese Entfernung zurückzulegen, nur in der Einheit Sekunden und Lichtsekunden unterscheidet, der Betrag ist aber der selbe. Messen wir das nur mit einer Uhr ist es einfach und für alle Beobachter ein eindeutiger Wert der der halben Zeit für Hin- plus Rückweg entspricht. Messen wir nur den einfachen Weg mit zwei Uhren, ist der Wert aber abhängig von der räumlichen Synchronisation der Uhren, die nicht für alle Beobachter gleich sein muss.

Für den Hinweg eines Zeitsignals, der der Bewegungsrichtung vom kreisenden Ring entsprechen soll, wird der Weg relativ zum ruhenden Ring mit A und relativ zum kreisenden Ring mit a bezeichnet. Für die entgegengesetzte Richtung entsprechend mit B und b.

Der Umfang des ruhenden Rings wird mit U und der Umfang des bewegten Rings mit u bezeichnet.

  U_R = (A_R + B_R) / 2

Da im ruhenden Ring die Blitzanteile den Beobachter aus beiden Richtungen wieder gleichzeitig erreichen ist hier:

  U_R = A_R = B_R

Da vom ruhenden Ring aus der Bewegte Ring die gleichen Raummaße annimmt ist: U_R = u_R

Da es im bewegten Ring zur Längenkontraktion kommt, ist: u_K = U_R / Wurzel(1 – v² / c²).

Die Tangentialgeschwindigkeit mit der sich der kreisende Ring bewegt ist v und wird in c angegeben. Den Lorentz­transformationen entsprechend messen zwei zueinander bewegte Beobachter die Geschwindigkeit des anderen jeweils gleich groß. Also braucht v nicht unterschieden zu werden.

Die Zeit aR bis der Blitz den auf dem Ring mitbewegten Beobachter in Bewegungsrichtung erreicht, kann so errechnet werden:

  v * a_R + U_R = y und c * a_R = y                          Also

  U_R = c * a_R – v * a_R = (c – v) * a_R                      Damit

  a_R = U_R / (c – v)                                                                                                                       (1)

Für die entgegengesetzte Richtung gilt:

  U_R = c * b_R + v * b_R = (c + v) * b_R                    Damit

  b_R = U_R / (c + v)                                                                                                                      (2)

Die vom ruhenden Ring aus gemessene Zeitdifferenz m_R für das Eintreffen der Blitzanteile beim kreisenden Beobachter ist:

  m_R = (a_R – b_R)                                                                                                                         (3)

Unter Berücksichtigung der Zeitdilatation beträgt die vom kreisenden Ring gemessene Zeitdifferenz:

  m_K = m_R * Wurzel(1 – v² / c²)                                                                                                 (4)

 

Das betrifft den vollständigen Ring. Um uns der Länge des Balkens, der gedreht werden soll, zu nähern, berücksichtigen wir zunächst die Längenkontraktion. Der bewegte Ring verkürzt sich, so dass eine Lücke entsteht. Vom ruhenden Ring aus gemessen beträgt die Länge des bewegten Rings, mit bR bezeichnet, nur noch:

  bR_R = U_R * Wurzel(1 – v² / c²)                                                                                                (5)

Durch die entstehende Lücke können die Zeitsignale nicht mehr zum Bewegten Beobachter zurückkehren. Bisher haben wir den Ring in beiden Richtungen genutzt., also eine doppelte Ringlänge. Jetzt teilen wir den Ring genau gegenüber von dem den Blitz aussendenden Beobachter. Deshalb müssen wir die Zeiten für die Lichtausbreitung halbieren ( * 0,5) und damit auch das Ergebnis mR. Vom Prinzip her ändert sich sonst nichts.

Für die Werte dieses Teilabschnitts, nR und bRR, und die Werte des ganzen Rings, mR und UR, besteht das Verhältnis:

  n_R / (m_R * 0,5) = bR_R / U_R                                                   │ersetzen wir darin bR_R Formel (5)

  n_R / (m_R * 0,5) = U_R * Wurzel(1 – v² / c²) / U_R                      │kürzen wir U_R und multiplizieren mit (m_R * 0,5)

  n_R = (m_R * 0,5) * Wurzel(1 – v² / c²)                                                                                       (6)

Berücksichtigen wir die Zeitdilatation, dann entspricht die im bewegten Ringabschnitt gemessene Zeitdifferenz n_K :

  n_K = n_R * Wurzel(1 – v² / c²)                                                 │ersetzen wir n_R Formel (6)

  n_K = m_R * 0,5 * Wurzel(1 – v² / c²) * Wurzel(1 – v² / c²)          │ersetzen wir m_R Formel (3)

  n_K = (a_R – b_R) * 0,5 * (1 – v² / c²)                                           │ersetzen wir a_R und b_R Formel (1+2)

  n_K = (U_R / (c – v) - U_R / (c + v)) * 0,5 * (1 – v² / c²)

Aus den Lorentz­transformationen geht hervor, dass sich ein Körper auch nach einer Beschleunigung weiterhin mit der gleichen Länge misst. Das entspricht auch dem Relativitätsprinzip der SRT. Damit ist die Länge des beschleunigten Ringabschnitts bRK vom kreisenden Ring aus gemessen: bRK = UR.
In die Formel eingesetzt:

  n_K = (bR_K / (c – v) – bR_K / (c + v)) * 0,5 * (1 - v² / c²)                                                              (7)
 

Diese Werte werde alle nur noch vom kreisenden Ring aus gemessen. Die Länge des Balkens kann hier einfach bestimmt werden und entspricht der Hälfte der Zeit die ein Lichtsignal für Hinweg plus Rückweg braucht in Lichtsekunden. Entwickeln wir zunächst eindeutige Ereignisse aus Sicht des ruhenden Rings und sehen wie beim Drehen des Balkens auf dem kreisenden Ring die Ereignisse widerspruchsfrei aufgehen.

Jetzt setzen wir die Uhren A(w) und K(w) zusammen auf das westliche Ende eines Balkens und die Uhren A(o) und K(o) auf das östliche Ende. An diesen Orten sollen jeweils die Uhren A(sw) und A(so) auf dem Ring montiert sein und dort zurückbleiben, wenn der Balken gedreht wird.

Die Uhren A(w) und K(w) befinden sich bei A(sw) am selben Ort und zeigen deshalb auch die gleiche Zeit an und ihre jeweiligen Zeitsignale 1 breiten sich mit einer einheitlichen Front aus. Für die sich im Bereich des anderen Balkenendes befindenden Uhren A(so), A(o) und K(o) gilt entsprechendes.

Die Uhren sollen räumlich der UTC entsprechend synchronisiert werden. Der Abstand zwischen W und O soll mit ihren Uhren gemessen a Lichtsekunden betragen.

Die von einer Uhr angezeigte Zeit soll z.B. für die Uhr A(sw) zur Zeit 1 als A(sw)[1] dargestellt werden. Das zu dem Zeitpunkt ausgesendete Zeitsignal als a(sw)[1]. Die mit ihnen zusammen ausgesendeten Zeitsignale der an ihrem Ort befindlichen Uhren werden durch ein + angefügt.

Also z.B. a(sw)[1] + a(w)[1] + k(w)[1].

Die Zeitsignale sollen am anderen Ende reflektiert werden und mit den Zeitsignalen der sich dort befindenden Uhren zurückgeschickt werden. Die Zeiten der dortigen Uhren werden ebenfalls mit + in einer neuen Zeile angefügt.

Senden die Uhren A(so) und A(sw) ihr Zeitsignal 1 aus, dann trifft das von der Uhr A(so) in westliche Richtung gesendete Zeitsignal 1 bei bei der Uhr A(sw) um 1 + a - n Sekunden ein. Das in östlicher Richtung gesendete Zeitsignal der Uhr A(sw) bei der Uhr A(so) um 1 + a + n Sekunden. Die Werte für a und n werden jeweils in der Eigenzeit einer Uhr gemessen. Das eindeutige Ereignis am westlichen Ende des Balkens sieht beim Eintreffen des Zeitsignal 1 so aus:

Wie die Abfolge der eindeutigen Ereignisse aussieht ist in der nachfolgenden Tabelle dargestellt. Die von den Uhren angezeigten Uhrzeitwerte und die Bewegungen der Zeit-Lichtsignale werden aus der Sicht des nicht rotierenden Rings berechnet.

Beginnen wir mit der UTC Zeit [1]:

Eintreffen der Zeitsignale am westlichen Ende zur UTC Zeit [1+a-n]:

Eintreffen der Zeitsignale am östlichen Ende zur UTC Zeit [1+a+n]:

Eintreffen der Reflektierten Zeitsignale zur UTC Zeit [1+2a]:

Von alle Uhren aus gemessen braucht das Zeitsignal a(o)[1] nach Westen (a – n) Sekunden und das Zeitsignal a(w)[1] nach Osten (a + n) Sekunden. Entsprechend umgekehrt die Zeiten für den Rückweg.

Drehen wir jetzt den Balken um. Dann sind die Uhren K(w) und K(o) weiterhin synchron mit den die UTC repräsentierenden Uhren A(sw) und A(so). Die Uhr A(w) geht gegenüber der UTC aber um n Sekunden nach, da sie auf dem Weg nach Osten langsamer gegangen ist und die Uhr A(o) gegenüber der UTC um n Sekunden vor, da sie auf dem Weg nach Westen schneller gegangen ist. Das Umdrehen soll d Sekunden dauern.

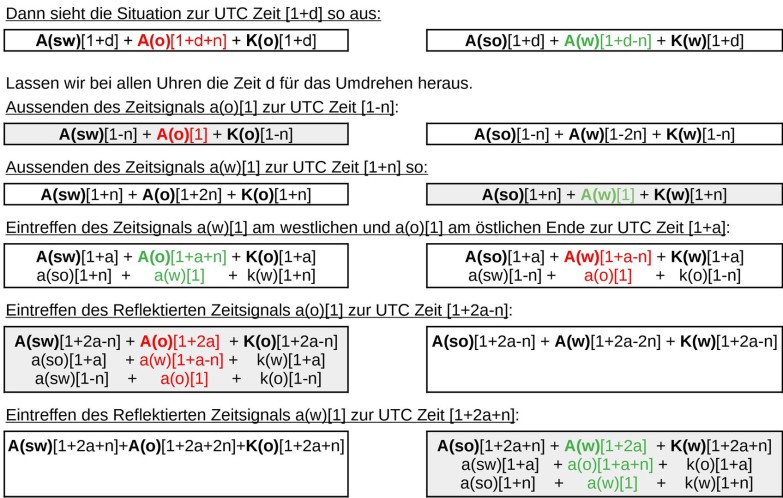
Dann sieht die Situation zur UTC Zeit [1+d] so aus:

Betrachten wir nur das Uhrenpaar A(w) und A(o). Vor dem Umdrehen trifft das Zeitsignal [1] der Uhr A(o), also a(o)[1], schon zum Ereignis A(w)[1+a-n] bei A(w) ein und nicht erst zur halben Zeit von 2a, was A(w)[1+a] entsprechen würde. Das Zeitsignal [1] der Uhr A(w), also a(w)[1], trifft erst zum Ereignis A(o)[1+a+n] bei der Uhr A(o) ein und nicht schon zum Ereignis A(o)[1+n].

Durch die räumliche Synchronisation der Uhren A(w) und A(o) entsprechend der UTC, wird eine längere Zeit für das Signal von A(w) nach A(o) als umgekehrt gemessen.

Durch das Umdrehen ändert sich nichts daran. Weiterhin trifft das Zeitsignal a(o)[1] bei A(w)[1+a-n] ein und das Zeitsignal a(w)[1] bei A(o)[1+a+n]. Die Zeitsignale treffen bei den Uhren unverändert ein. Die Uhren messen jetzt für die Westrichtung eine längere Zeit als für die Ostrichtung, was kausal aber falsch ist. Es kommt nur durch die jetzt nicht mehr mit der UTC synchrone Einstellung der Uhren A(w) und A(o) zustande. Würden zwei Laser, die ein den Lichtuhren entsprechendes Verhalten zeigen, ihre Strahlen sich gegenseitig zusenden, käme es während des Umdrehens zu keiner Verschiebung des Interferenzmusters.

Um die Uhren A(w) und A(o) nach Einsteins Gleich­zeitigkeits­definition miteinander räumlich zu synchronisieren, so dass von ihnen die von den Zeitsignalen gebrauchte Zeit für beide Richtungen gleich groß gemessen wird, können wir z.B. die Uhr A(o) um den Betrag n zurückstellen.

Dann sehen die Startereignisse zur UTC Zeit [1], bei der auch A(w) das Zeitsignal a(w)[1] aussendet, so aus:

Zum Zeitpunkt wo A(o) sein Zeitsignal a(o)[1] aussendet, also zur UTC Zeit [1+n] so:

Eintreffen des a(o)[1] Zeitsignals am westlichen Ende zur UTC Zeit [1+a]:

Eintreffen des Zeitsignals a(w)[1] am östlichen Ende zur UTC Zeit [1+a+n]:

Eintreffen der Reflektierten Zeitsignals a(w)[1] zur UTC Zeit [1+2a]:

Eintreffen des reflektierten Zeitsignals a(o)[1] zur UTC Zeit [1+2a+n]:

Betrachten wir wieder nur die Uhren A(w) und A(o). Bei dieser räumlichen Synchronisation der Uhren messen sie für die Dauer, die die Zeitsignale sowohl in Ost- als auch in Westrichtung brauchen, eine gleichlange Zeit, nämlich die Hälfte von 2a, also a.

Drehen wir jetzt den Balken um, was d Sekunden dauern soll, dann sieht die Situation zur UTC Zeit [1+d] so aus:

Die Uhr A(o) ist auf dem Weg nach Westen um n Sekunden schneller gegangen. Damit ist sie wieder synchron mit der UTC, nachdem sie vorher gegenüber der UTC um n Sekunden nach gegangen ist. Die Uhr A(w) ist auf dem Weg nach Osten um n Sekunden langsamer gegangen und geht damit zur UTC jetzt um n Sekunden nach. Von dieser Situation ausgehend sieht die Abfolge genauso aus wie im vorhergehenden Beispiel. Und auch hier ändert sich das Eintreffen der Zeitsignale nicht durch das Umdrehen.

Für alle Beobachter brauchen die Signale für Hin- und Rückweg gemeinsam 2a Sekunden. Aus der räumlichen Synchronisation der Uhren A(w) und A(o) nach Einsteins Gleich­zeitigkeits­definition wird für Hin- und Rückweg die gleiche Zeit gemessen, was sich durch das Umdrehen des Balkens nicht ändert. Bei der Rotation ist diese räumliche Gleichzeitigkeit aber nicht mit den sich am Himmel wiederholenden Beobachtungen, den über den restlichen Ring versendeten Zeitsignalen oder dem Uhrentransport über den restlichen Ring vereinbar.

Damit kann man bei der Rotation durch eindeutige Messergebnisse die räumliche Synchronisation nach Einsteins Gleich­zeitigkeits­definition kausal als falsch widerlegen.

Hätte man die Möglichkeit eine Information mit einer höheren als der Licht­geschwindig­keit weiter zu geben, dann könnte man die räumliche Gleichzeitigkeit stärker einengen als mit Lichtsignalen. Damit wäre auch bei der geradlinigen Bewegung Einsteins Gleich­zeitigkeits­definition kausal als falsch zu widerlegen.

Hält man die Postulate der Speziellen Relativitäts­theorie für tatsächlich so in dem uns umgebenden Universum als gegeben, dann kann es keine höhere als die Licht­geschwindig­keit geben. Selbstverständlich kann es dann auch keinen WARP Antrieb oder Wurmlöcher geben. Zumindest keine Wurmlöcher die in unser Universum zurückführen. Ob ich eine Information mit Überlichtgeschwindigkeit versende oder mit einem Raumschiff mit WARP Antrieb transportiere macht kausal keinen Unterschied.

Gehen wir aus von der Situation, bei der alle Uhren synchron sind in der UTC. Nach dem Umdrehen des Balkens geht die Uhr A(o) nicht nur um n_K Sekunden gegenüber der UTC vor, sondern auch gegenüber der Uhr K(o). Und die Uhr A(w) geht nicht nur gegenüber der UTC um n_K Sekunden nach, sondern auch gegenüber der Uhr K(w). Die Zeitdifferenz n_K, die sich zwischen K(w) und A(w) entwickelt ist nur abhängig von dem Weg, den sie in Ost-West Richtung zurücklegen und der Tangentialgeschwindigkeit mit der sich der Ring dreht.

Wie sehen die Ergebnisse aus, wenn dieser Ring jetzt auf einem größeren Ring C montiert wird, der der Erdbahn um die Sonne entspricht. Auch auf diesem Ring werden die Uhren der UTC entsprechend räumlich synchronisiert. Hier wollen wir die Zeit UTC_S nennen. Die Zeit der auf dem kleinen Ring B stationären Uhren UTC_E.

Logischerweise verhalten sich die Uhren auf dem Ring B wie im vorherigen Beispiel die Uhren auf dem Balken, den man hier nur ständig weiter dreht. Auch hier gehen die Uhren in der UTC_E bei Bewegung in Richtung der Erdbewegung gegenüber den Uhren der UTC_S langsamer und in entgegengesetzter Richtung schneller. Das hat aber genauso wie beim Balken keinen Einfluss auf das Eintreffen der Zeitsignale innerhalb des Rings B, soweit Aussende- und Empfangszeitpunkt mit Licht- oder Atomuhren gemessen werden.

Da sich die K-Uhren aber nicht den Lorentz­transformationen entsprechend verhalten, entsteht zwischen den Atomuhren und den neben ihnen stehenden K-Uhren eine Zeitdifferenz mit einer sinusförmigen Veränderung. Dafür zeigen sie ein dem Balkenbeispiel entsprechendes Verhalten, also keine Veränderung zu den Uhren der UTC_S.

Die Erdbahn kreist aber mit der Sonne um das Zentrum der Milchstraße. Wird unser Beispiel um einen entsprechenden Effekt erweitert, dann kommt es zu einer sinusförmig schwankenden Zeitdifferenz zwischen den K-Uhren und der UTC_S. Diese würde die Kurve der Zeitdifferenz zwischen der UTC_E und den K-Uhren noch überlagern. Wir hätten also frühestens erst nach einem Jahr eine vergleichbare Kurve für die Schwankung der Zeitdifferenz.

Gibt es bei den mit Atomuhren erzielbaren Messwerten einen Unterschied zu Inertialsystemen?

Betrachten wir von einer Zylinderfläche (Zylinderdurchmesser das dreifache des Milchstraßendurchmessers) nur einen Ausschnitt mit der Kantenlänge von einer Astronomischen Einheit. In diesem Ausschnitt werden die Uhren nach Einsteins Gleich­zeitigkeits­definition räumlich synchronisiert. Unter diesen Bedingungen bestehen für den Gang der Uhren und die Ausbreitung von Lichtsignalen die Verhältnisse wie in einem Inertialsystem. Lassen wir sich zwei oder mehrere Zylinderflächen aneinander vorbei bewegen und betrachten nur die Atomuhren und Zeit-Lichtsignale, dann entsprechen die Messergebnisse und Berechnungen exakt den Verhältnissen von Inertialsystemen. Wir könnten aber immer noch Signale entlang des Zylinders senden, auch wenn das einige Jahrmillionen dauern würde. Damit könnten wir Messungen erzeugen, die die räumliche Synchronisation der Uhren nach Einsteins Gleich­zeitigkeits­definition kausal als falsch darstellen würden.

Erst wenn wir diese Fläche vom Zylinder lösen, haben wir tatsächlich eine geradlinige Bewegung, auch wenn diese sich von der anderen Bewegung kaum messbar unterscheidet. Damit ist auch die Zentrifugalkraft weg. Auch ist fraglich ob ein Zeitsignal, das wir in der einen Richtung durchs Universum schicken uns aus der anderen Richtung wieder erreichen würde. Wir können aber immer noch das Universum an uns vorbeiziehen sehen. Allerdings gibt es keine Beobachtungen am Himmel die sich wiederholen.

Isolierte theoretische Überlegungen haben einen besonderen Mangel. Sie haben keine Bezug zu der uns umgebenden Realität. Betrachten wir 2 Raumfahrer, die sich geradlinig mit halber Licht­geschwindig­keit aneinander vorbei bewegen. Nach der SRT sollen sie gleichberechtigt sein. Aber wie sieht es aus, wenn wir das in der Realität durchführen?

Der eine befindet sich noch auf dem Raumschiff Erde. Er sieht ein Universum um sich, das in alle Richtungen etwa gleich aussieht. Aus allen Richtungen erreicht ihn etwa die gleiche Strahlung. In diesem Universum sieht er den anderen Raumfahrer sich mit halber Licht­geschwindig­keit an ihm vorbei bewegen.

Der andere Raumfahrer sieht ihn auch mit halber Licht­geschwindig­keit an sich vorbei ziehen, aber mit ihm zusammen sieht er ein ganzes Universum an sich vorbei ziehen. Dieses sieht auch nicht in allen Richtungen gleich aus. In der einen Richtung ist es rotverschoben. Aus dieser Richtung erhält er nur sehr wenig energiearme Strahlung. In der anderen Richtung ist es blauverschoben. Aus dieser Richtung wirkt massiv hochenergetische Strahlung auf ihn ein. Diese Strahlung muss zwangsläufig sein Raumschiff in Richtung der Bewegung des Universums beschleunigen. Mit empfindlichen Messinstrumenten sollte das auch innerhalb des Raumschiffs zu messen sein.

Wenn die Situation auch etwas anders ist, so können wir doch schon heute so präzise Messen, dass man die Pioneer-Anomalie feststellen konnte. Die Ursache war ein nur sehr geringer Unterschied in der Berechnung der empfangenen und der abgestrahlten Energie. Der auf den Raumfahrer einwirkende Strahlungsunterschied sollte deutlich größer sein.

Kann man hier wirklich beide Raumfahrer für gleichberechtigt halten, nur weil sie sich beide, bei isolierter Betrachtung, theoretisch und mathematisch jeweils in einem Inertialsystem befinden?

Wer mag mit mir den großen Schritt gehen und die absolute Konstanz der Licht­geschwindig­keit in Frage stellen und annehmen sie wäre konstant zum Gravitationsfeld?

Wer mag auch noch annehmen, das Gravitationsfeld, gebildet aus den sich überlagernden Feldern der Masseteilchen, wäre ein in seiner Wirkung plastisch verformbares Feld? Dann könnten die Merkur-Anomalie und der Schiff-Effekt nicht nur Überlagerungen des Gravitationsfeldes sein, so wie Einstein es deutete, sondern plastische Veränderungen des Feldes. Das würde auch bedeuten, dass die Erde auf ihrem Weg um die Sonne das Gravitationsfeld gering verformt und mitnimmt, was die Fly-by-Anomalie bewirkt. Der Effekt könnte noch größer werden, wenn sich die lokal das Gravitationsfeld bestimmenden Massen in einer gemeinsamen Richtung bewegen. Das Gravitationsfeld bewirkt die Zentrifugalkraft. Wenn dieses aber bei rotierenden Galaxien etwas mitrotiert, sieht es von außen aus, als ob sich die Sterne zu schnell bewegen. Es ist aber für das herrschende Gravitationsfeld genau die richtige Geschwindigkeit, auch ohne dunkle Materie.

Ich würde das für die einfachere Lösung und damit nach Ockham’s razor für die richtige halten.

Welcher Mathematiker mit Zugang zu den astronomischen Daten mag diese Lösung prüfen?

Ausführlicheres ist in meinem Buch zu finden: Die Relativität des Beobachers und die Gravitation.

Es ist auch im Ausland erhältlich:    deutsch ISBN: 978-3-7557-1725-6

english: The Relativity of the Observer and the Gravitation ISBN: 978-3-7557-4026-1