Lecture 1.9.2021

A method for measuring the linear movement relative to the gravitational field.

Good afternoon, ladies and gentlemen

In this lecture I will only limit myself to the essential points. I had already published the basic idea on the Internet because 15 minutes are too short to show it. This version has also suffered from time. The full version you can find on my homepage.

At the beginning I would like to ask a question:

Have we already understood relativity correctly?

Measured values ​​are always a comparison of 2 physical phenomena. This means that the measured values ​​are inevitably as relative as this comparison. But does this relativity also apply to what we actually want to measure?

When we observe space, gases gather into stars, stars into galaxies, and galaxies into galaxy clusters. Matter moves closer together and the mass-free spaces in between become larger.

But why should the distance between the earth and the sun increase about 15 cm per year? The moon is said to move away from the earth by 3.8 cm per year. If you extrapolate that to a distance of 13 billion light years, you get a speed of 380,000 km/s, which roughly corresponds to the escape speed of the galaxies at this distance.

But when space doesn't expand at all, but rather time speeds up. Then the spectral lines would have a much higher level today than they used to have. In the light of the distant stars, this state would then be frozen a long time ago and would have nothing to do with space expansion. I think that would be more compatible with what we see in space.

Let's get to my idea.

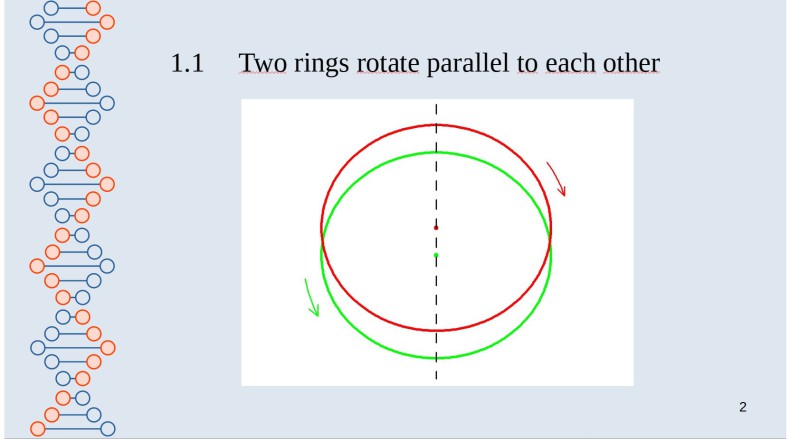
First: Let us imagine two ring frames, far away from other masses that circle parallel to each other. Let's call them A and B. No centrifugal force is measured at the edge of ring A. If the diameter of the rings and the angular velocity are known, the centrifugal force at the edge of the ring B can be calculated. But does a centrifugal force have to be measured at the edge of ring B at all? Is it measured because it can be calculated? Does the math dictate what happens on the other ring? If so, what determines that it is not exactly the other way round and that the centrifugal force occurs in ring A? Because I said that?

If the empty space is indeed empty, then for me there is no reason why there should be centrifugal force at all. The observations show, however, that a centrifugal force occurs at the edge of every body that rotates towards the universe. This is only possible if there is something locally that causes this force. I call it a gravitational field.

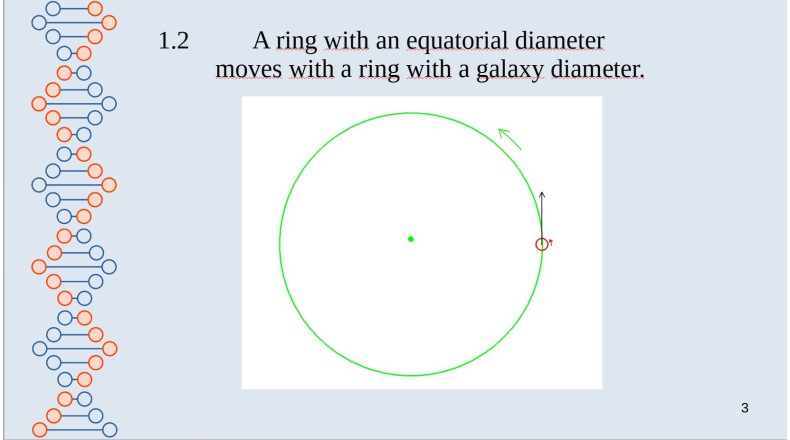
Let's imagine the rings have the diameter of the equator. Then we could mount this on a ring whose diameter corresponds to that of our galaxy. The same laws must also apply to this ring and the centrifugal force must be measured accordingly. To that what creates this centrifugal force, rings A and B move sideways. Their center moves almost in a straight line. No matter what creates the centrifugal force. Against that you can rotate, but you can also move in a straight line. Far away from gravitational masses, this also corresponds to an inertial movement.

Second: Let us let cylinder surfaces move past each other. Let us only consider sections of the cylinder surfaces. In these areas the clocks should be spatially synchronized according to Einstein's definition of simultaneity. Now we only measure the rate of the atomic clocks and the movement of time-light signals that are sent directly to each other by the observers. Then we have exactly the same conditions as the Special Theory of Relativity (SRT) describes for inertial systems.

But here we can measure the centrifugal force to determine a preferred state of rest.

In addition, there is the possibility not only to move clocks back and forth between the observers, but also to move them further over the rest of the ring. In this way one can causally establish that the clocks run fastest on the ring, which does not rotate to the surrounding universe. In this way, a preferred idle state can also be determined.

We can also not only send the time-light signals back and forth between the observers, but also across the rest of the ring. Only in the case of the non-rotating ring do the light signals arrive again at the sending observer from both directions at the same time. A preferred resting state can also be determined in this way.

As soon as rotation comes into play, these possibilities can be used to causally show that spatial simultaneity cannot correspond to Einstein's definition of simultaneity. That's why it doesn't do it in Universal Time Coordinated (UTC).

The three mentioned possibilities to determine the movement do not exist with the linear movement. So should the physical conditions be fundamentally different?

An example of this. Imagine the large ring 200,000 light years across. The edge of the ring is said to move at half the speed of light. Then the centrifugal force is so low that I can still hold onto myself and a beam with two observers at the ends with my hand. We all have atomic clocks. If I hold on to the ring, the spatial simultaneity corresponds to a simultaneity corresponding to the UTC for this ring. If I let go, it should correspond to Einstein's definition of simultaneity and the observers at the ends of the bar have to adjust their clocks. If I hold on tight again, it corresponds to UTC again and the observers have to adjust their clocks again. What is changed here by holding on or not holding on? Is the spatial simultaneity actually changed, or is only the measuring instruments adjusted and thus the measured value. What really makes sense here?

Third: With the rotation, the twin paradox is easily resolved.

Let us synchronize 2 clocks along the equator according to Einstein's definition of simultaneity. Then we move a clock back and forth between these clocks. For this relative movement, the clocks stationary at the equator measure the moving clock slower, like it is calculated by the Lorentz transformations. This applies to moving in the east as well as in the west direction. If the clock is moved slowly, this effect is negligible. The relative considerations here also correspond to inertial systems.

But we know that the moving clock actually goes much slower on the way to the east and actually goes faster on the way to the west than the clocks on the equator, at least as long as the western relative movement is not greater than twice the speed of the tangential movement on the equator. This is also measured in the correct spatial synchronization of the UTC.

The moving clock could be on one end of a long railroad car and a second clock on the other. If these clocks are synchronized with each other according to Einstein's definition of simultaneity, they measure the stationary clocks slower, according to the Lorentz transformations. It does not matter whether you move past the clocks in an east or west direction. However, if the railroad car accelerates with the expenditure of energy in order to drive back again, the clocks have to be reset afterwards in order to meet Einstein's definition of simultaneity again.

If the measuring instruments are adjusted during the test, can the two phases still be compared with one another? If he does not adjust his clocks after accelerating for the reversal, then he also measures the clocks stationary on the ring as going faster. In total, exactly the time that results in the twin paradox for the reversing twin.

If each pair of clocks, one stationary on the ring and the other in the railroad car, is synchronized according to Einstein's definition of simultaneity, they each measure the other as would be calculated with the Lorentz transformations, but they have actually a different speed against that what causes the centrifugal force.

I think that is not fundamentally different with rectilinear or inertial motion.

Fourth: Let us come to the special field of ether.

The ether was supposed to have special properties that could not be determined, so it was rightly rejected. The interpretation of the Michelson-Morley experiment (MME) is often presented somewhat distorted today, because it does not refute the fact that the moving of light can be constant to a reference field. An observer can also move to a reference field, but then the speed of light would not be constant to the observer. As already described above, there is a preferred field of rest during rotation, which I call a gravitational field.

Anyone who can imagine something as strange as dark matter should also be able to imagine that mass particles can move up to the speed of light against the gravitational field and massless light photons can move exactly at the speed of light, without this field has necessarily to have other properties. This then applies to the rotation as well as to the linear movement.

Fifth: What do clocks have to do with time?

I would like to start with another example. I determine the mass of bodies with the help of a beam balance and a spring balance. Then I repeat that on the moon. The beam balance delivers the same measurement results, the spring balance does not. Here, too, I ask: What do the measuring instruments have to do with the mass? Due to the change in the environment, the measuring instruments with different measuring principles are influenced differently. But does this mean that one measuring instrument has more to do with the mass than the other?

Now related to the time. I measure the time with a light clock and a pendulum clock. Then I go up the mountain and repeat the measurement. Here I notice that the light clock goes faster and the pendulum clock slows down. But does one of the clocks have more to do with time than the other? I do not think so. The clocks have different measuring principles. As a result, they are also influenced differently by changes in the environment.

With the beam balance, the mass measures itself, so to speak, with itself. Therefore, the change in the environment does not lead to any change in the measured values. With the light clock, the movement of light is measured with itself and the steady movement of light is the basis of the geometry of the Lorentz transformations. As a result, the light clock also constantly measures the time in the geometry of the Lorentz transformations. The atomic clocks also measure time on the basis of light and have the same timing as light clocks.

Again to the question: What do clocks have to do with “time itself”? Are there different times, e.g. local times? This certainly applies to the measuring instruments, as clocks or scales, but I don't think that applies to what we actually want to measure: “Time itself”.

With the pendulum clock, there is a physical time measurement principle that reacts differently to changes in the environment than atomic clocks. But this is also dependent on gravitation or mass movement. We have to try to find a physical phenomenon that has a sufficiently fast cycle, like the atomic clock, but which is independent of the gravitational field. So it has the same rhythm on the mountain as in the valley. And that transported in an east or west direction around the earth maintains the same rhythm. I will call them k-clocks.

If one were to find such a phenomenon, one would initially have a problem synchronizing these clocks. It is crucial that these k-clocks all have the same timing. This could then be used to define a time like the international system second. I would like to call this part of time K-unit.

In the spatial synchronization of the atomic clocks in UTC, the value of the measured speed of light is not the same speed in east and west directions. Here I assume that the interested audience has read the article on my homepage. Therein the following is described in more detail.

If I fix 2 atomic clocks on the ends of a bar and turn the bar, this does not lead to any shifting of the arrival of the time signals between these clocks. However, there is a shift against the UTC time signals. Not only because of the changed transit time of the signals, but also because the clock moving westwards when the bar is turned goes faster on this path and the clock moving eastwards is significantly slower.

If I do the same with K-clocks, there is a shift against the UTC due to the change in the running time of the time signals, but also a shift in the arrival of the time signals between the K-clocks.

The earth not only rotates and moves around the sun, but also the sun around the center of the Milky Way and this should also move. The speed against the gravitational field is decisive for the shift in the arrival of the time signals between the K-clocks. This of course changes with the movement of the earth.

If the K-clock B is in the direction of the movement towards the gravitational field, the time difference for the arrival of the time signals from K-clock B at K-clock A is the smallest. If the K-clock B is in the opposite direction, the time difference is greatest. In this way, the direction of the movement against the gravitational field can be determined. The speed against the field can be calculated from the size of the change in the time difference and the distance between the clocks. You can find the mathematical derivation on my homepage.

Final remark: Let us free the general theory of relativity from the dogma of the absolute constancy of the speed of light. Let us see the gravitational field as a field formed from the gravitational fields of the mass particles. Then this could be changed plastically by the mass particles witch are moved against it.

Einstein called the anomaly in the perihelion rotation of Mercury and the Schiff effect, which are explained by the general theory of relativity, as superpositions of the gravitational field. But if there are plastic changes, then the earth would also have to take the gravitational field with it a little in its movement, which explains the fly-by anomaly. In areas where the masses that locally determine the gravitational field move in a uniform direction, this could become even clearer, such as in galaxies. The moving masses cause the gravitational field to rotate. Since the gravitational field determines the centrifugal force, the movement of the stars is measured from the outside as too fast, although the movement relative against this local gravitational field is exactly correct, even without dark matter.

To do this, one may just have to apply the formulas of the general theory of relativity a little differently. But I'm not a mathematician and I can't solve that.

On the other hand, one could look for clocks that are not dependent on the gravitational field with only a small part of the effort with which one searches for dark matter.

Thank you